|
Bose-Einstein condensation is a strange phase transition. It was predicted by Einstein
in 1924 -- the first phase transition in the history of statistical mechanics -- for systems
of non-interacting bosonic quantum particles. It was not observed experimentally until 1995 by
Cornell, Wieman, and Ketterle (Nobel prize of physics, 1999). This phase transition is
believed to give rise to superfluidity and superconductivity; precise links
have yet to be established.
A major open question is about the effects of interactions on the critical temperature. Does it increase or decrease for interacting systems, compared to the ideal gas? The question has been controversial for several decades, until physicists reached a consensus in 2001-03: to first order, the change of critical temperature ΔT_c / T_c^0 is given by c a ρ1/3, with a the scattering length of the interaction potential between the particles, ρ the density, and c is a dimensionless universal constant equal to c = 1.3.
References
• Rigorous upper bound on the critical temperature of dilute Bose gases, with R. Seiringer, Phys. Rev. B 80, 014502 (2009)
• Critical temperature of dilute Bose gases, with V. Betz, Phys. Rev. A 81, 023611 (2010)
A major open question is about the effects of interactions on the critical temperature. Does it increase or decrease for interacting systems, compared to the ideal gas? The question has been controversial for several decades, until physicists reached a consensus in 2001-03: to first order, the change of critical temperature ΔT_c / T_c^0 is given by c a ρ1/3, with a the scattering length of the interaction potential between the particles, ρ the density, and c is a dimensionless universal constant equal to c = 1.3.
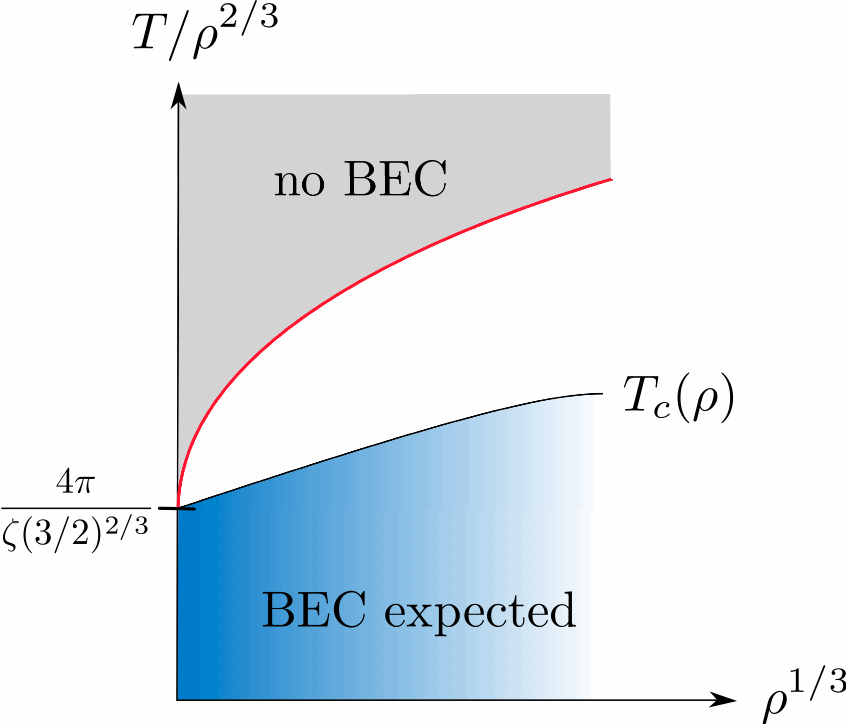 Phase diagram of dilute Bose gas |
With Robert Seiringer, we provided a mathematically rigorous bound for the critical temperature, by proving that there is no Bose-Einstein condensation when ΔT_c / T_c^0 is bigger than 5 times the square root of a ρ1/3. Here are the slides of a talk on this topic. |
| The constant above can be calculated using the model of "weighted spatial permutations". Volker Betz and I performed these calculations, finding c = -2.33. This result does not agree at all with the physicists' consensus! Although this result is not mathematically rigorous, we expect it to be correct. We do not know how to resolve the discrepancy with the previous calculations. Here are slides on this topic. |
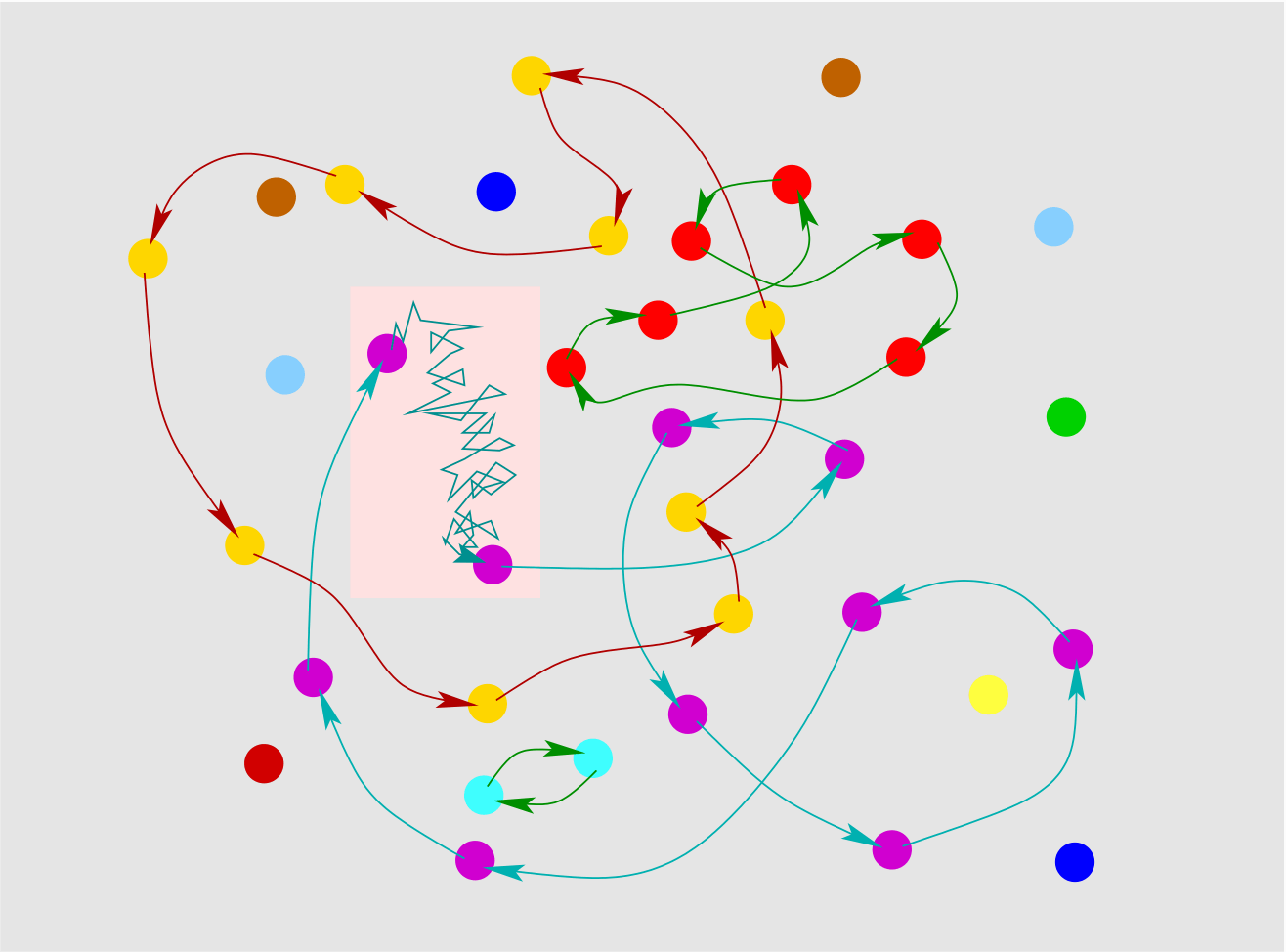 Illustration for spatial random permutations. Permutation jumps correspond to Brownian bridges |
• Rigorous upper bound on the critical temperature of dilute Bose gases, with R. Seiringer, Phys. Rev. B 80, 014502 (2009)
• Critical temperature of dilute Bose gases, with V. Betz, Phys. Rev. A 81, 023611 (2010)
The probability of permutations involves cycle weights.
That is, let (θ1,θ2,...) be nonnegative numbers, and let
αi defined by e-αi = θi.
We define the probability of a permutation π of n elements to be
P(π) ~ Πj>0 θjrj(π),
where rj(π) denotes the number of j-cycles in π. The normalization constant is missing. Our goal is to characterize the length L1 of the cycle that contains the index 1. Things depend on the cycle weights.
Let me describe the results in the case where αj = jγ. These were obtained in collaboration with V. Betz and Y. Velenik.
• Random permutations with cycle weights, with V. Betz, Y. Velenik
P(π) ~ Πj>0 θjrj(π),
where rj(π) denotes the number of j-cycles in π. The normalization constant is missing. Our goal is to characterize the length L1 of the cycle that contains the index 1. Things depend on the cycle weights.
Let me describe the results in the case where αj = jγ. These were obtained in collaboration with V. Betz and Y. Velenik.
- The case γ < 0 is close to the uniform distribution.
- In the case γ = 0, i.e. when θj --> θ (called the Ewens distribution), we find that P(L1 > sn) --> (1-s)θ.
- The case 0 < γ < 1 is surprising, as we find that almost all indices belong to a single giant cycle! We also prove two additional results: (i) there is a uniformly positive probability that all indices belong to a single cycle of length n; (ii) in some cases, finite cycles exist with uniformly positive probability. It would be nice to have more detailed results on the statistics of finite cycles.
- The case γ = 1 is actually equivalent to uniform permutations because of a tricky symmetry.
- When γ > 1 the cycles become shorter, and L1 behaves asymptotically as [(1-γ)-1 log n]1/γ.
• Random permutations with cycle weights, with V. Betz, Y. Velenik
Here are the slides of a talk on this topic.
References
• Spatial random permutations and infinite cycles, with V. Betz; Commun. Math. Phys. 285, 469-501 (2009)
• Spatial random permutations with small cycle weights, with V. Betz; Probab. Th. Rel. Fields (2010)
References
• Spatial random permutations and infinite cycles, with V. Betz; Commun. Math. Phys. 285, 469-501 (2009)
• Spatial random permutations with small cycle weights, with V. Betz; Probab. Th. Rel. Fields (2010)
The method of cluster expansions was introduced in the 1930's in statistical mechanics
in order to study gases of classical interacting particles. Its main achievement,
from the point of view of physics, may be the derivation of the van der Waals equation
of state for weakly interacting systems. The method was made rigorous by
mathematical-physicists in the 1960's, see the book of Ruelle ("Statistical Mechanics:
Rigorous Results", 1969) and references therein.
The method split afterwards. One branch involves continuous systems, with applications to classical systems (Penrose 1967, Minlos-Poghosyan 1977, Brydges-Federbush 1978), quantum systems (Ginibre 1971), or quantum field theory (Glimm-Jaffe-Spencer 1974, Malyshev 1980, Battle-Federbush 1982, Brydges-Kennedy 1987). The other branch involves polymer systems, i.e. discrete systems with additional internal structure (Gruber-Kunz 1971, Dobrushin 1996, Bovier-Zahradník 2000, Miracle-Solé 2000, Sokal 2001, Fernández-Procacci 2007). An important step forward was the article of Kotecký and Preiss in 1986 with its simplified setting and its elegant condition for the convergence of the cluster expansion. Important and useful surveys were written by Brydges (1986), Pfister (1991), Abdesselam and Rivasseau (1994).
The method of cluster expansions applies when the objects do not interact much; this the case when they are far apart (low density), or when interactions are weak. My first contribution to this topic, in 2004, was an extension of the Kotecký-Preiss criterion that takes into account these two aspects; it applies to both discrete and continuous systems. Recently, with Suren Poghosyan, we have proposed a general approach that applies to systems with repulsive or stable interactions (2009).
Here are slides on this topic.
References
• Cluster expansions & correlation functions, Moscow Math. J. 4, 511-522 (2004)
• Abstract cluster expansion with applications to statistical mechanical systems, with S. Poghosyan, J. Math. Phys. 50, 053509 (2009)
The method split afterwards. One branch involves continuous systems, with applications to classical systems (Penrose 1967, Minlos-Poghosyan 1977, Brydges-Federbush 1978), quantum systems (Ginibre 1971), or quantum field theory (Glimm-Jaffe-Spencer 1974, Malyshev 1980, Battle-Federbush 1982, Brydges-Kennedy 1987). The other branch involves polymer systems, i.e. discrete systems with additional internal structure (Gruber-Kunz 1971, Dobrushin 1996, Bovier-Zahradník 2000, Miracle-Solé 2000, Sokal 2001, Fernández-Procacci 2007). An important step forward was the article of Kotecký and Preiss in 1986 with its simplified setting and its elegant condition for the convergence of the cluster expansion. Important and useful surveys were written by Brydges (1986), Pfister (1991), Abdesselam and Rivasseau (1994).
The method of cluster expansions applies when the objects do not interact much; this the case when they are far apart (low density), or when interactions are weak. My first contribution to this topic, in 2004, was an extension of the Kotecký-Preiss criterion that takes into account these two aspects; it applies to both discrete and continuous systems. Recently, with Suren Poghosyan, we have proposed a general approach that applies to systems with repulsive or stable interactions (2009).
Here are slides on this topic.
References
• Cluster expansions & correlation functions, Moscow Math. J. 4, 511-522 (2004)
• Abstract cluster expansion with applications to statistical mechanical systems, with S. Poghosyan, J. Math. Phys. 50, 053509 (2009)




